What is a Hyperbola?

A hyperbola is a curve where the distances of any point from:

• a fixed point (the focus), and
• a fixed straight line (the directrix) are always in the same ratio.

Glossary

1. Focus: fixed point used to determine the eccentricity of a hyperbola.
2. Directrix: the line from which the hyperbola curves away from.
3. Eccentricity: the amount of variation in the conic section from being circular.
4. Major Axis: a line that passes through the center, vertices and focus of the hyperbola.
5. Minor Axis: a line perpendicular to the major axis that passes through the center of the hyperbola.

Equations

Hyperbola with Horizontal Major Axis

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Hyperbola with Vertical Major Axis

$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$

Equations

Asymptotes

$y=\pm \frac{b}{a}x$

Foci (plural of Focus)

$c=\pm \sqrt{b^2+a^2}$

Directrices

$x=\pm \frac{a^2}{\sqrt{a^2+b^2}}$

Graphing it on a TI-89/TI-84

From the standard form: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ we can derive:

1. $-\frac{y^2}{b^2}=1-\frac{x^2}{a^2}$
2. $-y^2=b^2-\frac{x^2{b}^2}{a^2}$
3. $y^2=-b^2+\frac{x^2{b}^2}{a^2}$
4. $y=\sqrt{-b^2+\frac{x^2{b}^2}{a^2}}$

Graphing it by hand

Real life examples

Dulles Airport

Dulles Airport is in the shape of a hyperbolic paraboloid.

Lampshade

A household lamp casts hyperbolic shadows on a wall.

Gear Transmission

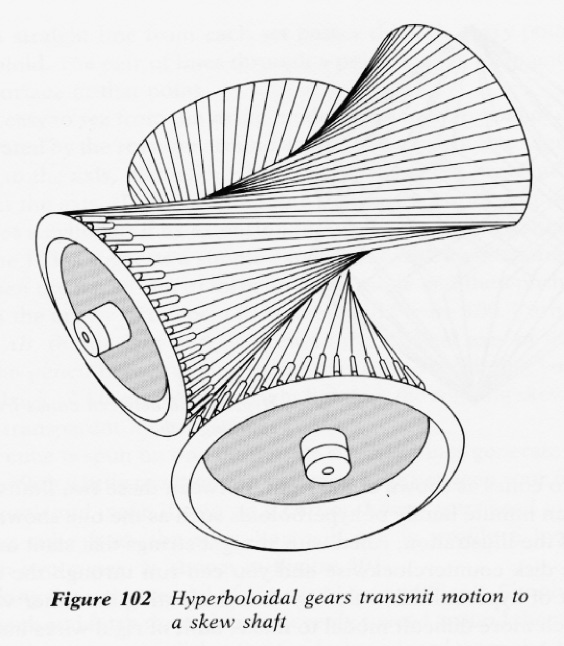
Two hyperboloids of revolution can provide gear transmission between two skew axes. The cogs of each gear are a set of generating straight lines.

Cooling Towers of Nuclear Reactors

The hyperboloid is the design standard for all nuclear cooling towers. When designing these cooling towers, engineers are faced with two problems:

1. the structutre must be able to withstand high winds and
2. they should be built with as little material as possible.

Satellites

Open orbits of comets about the sun follow hyperbolas

Activity Time!